3.4. Node Impurity and Tree Height#
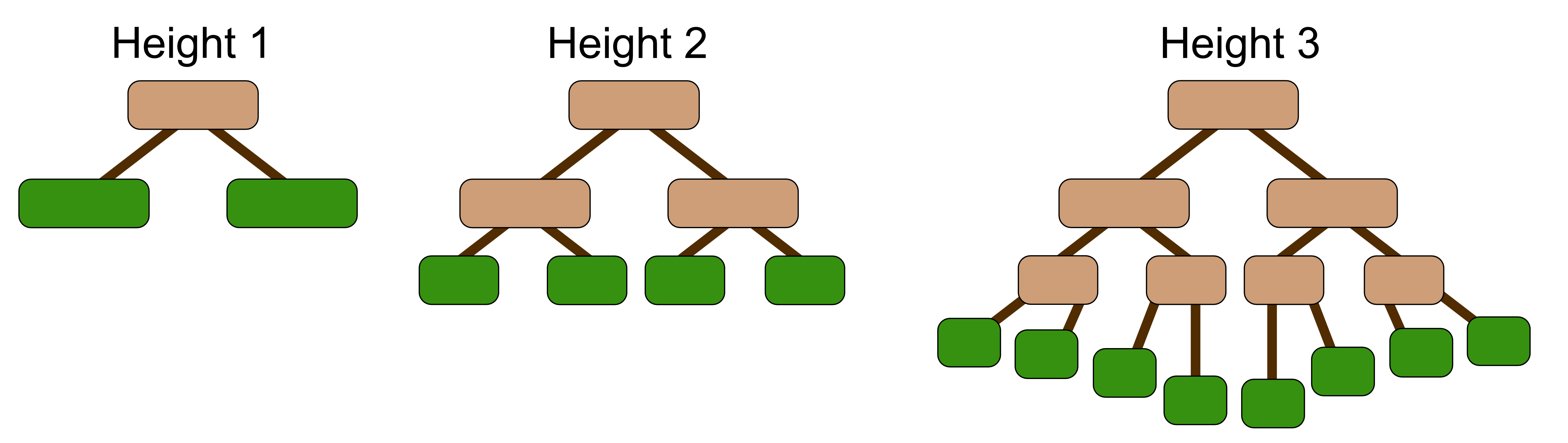
The size of a tree is typically measured by height. The height of the tree refers to the maximum number of decision points, i.e. nodes. from the root to any leaf node. Related to height is depth. The depth of a node is how far away the node is from the root. The root node is always at depth 0, which means that
for a tree of height 1, the leaves are at depth 1
for a tree of height 2, the leaves are at depth 2, and so on…
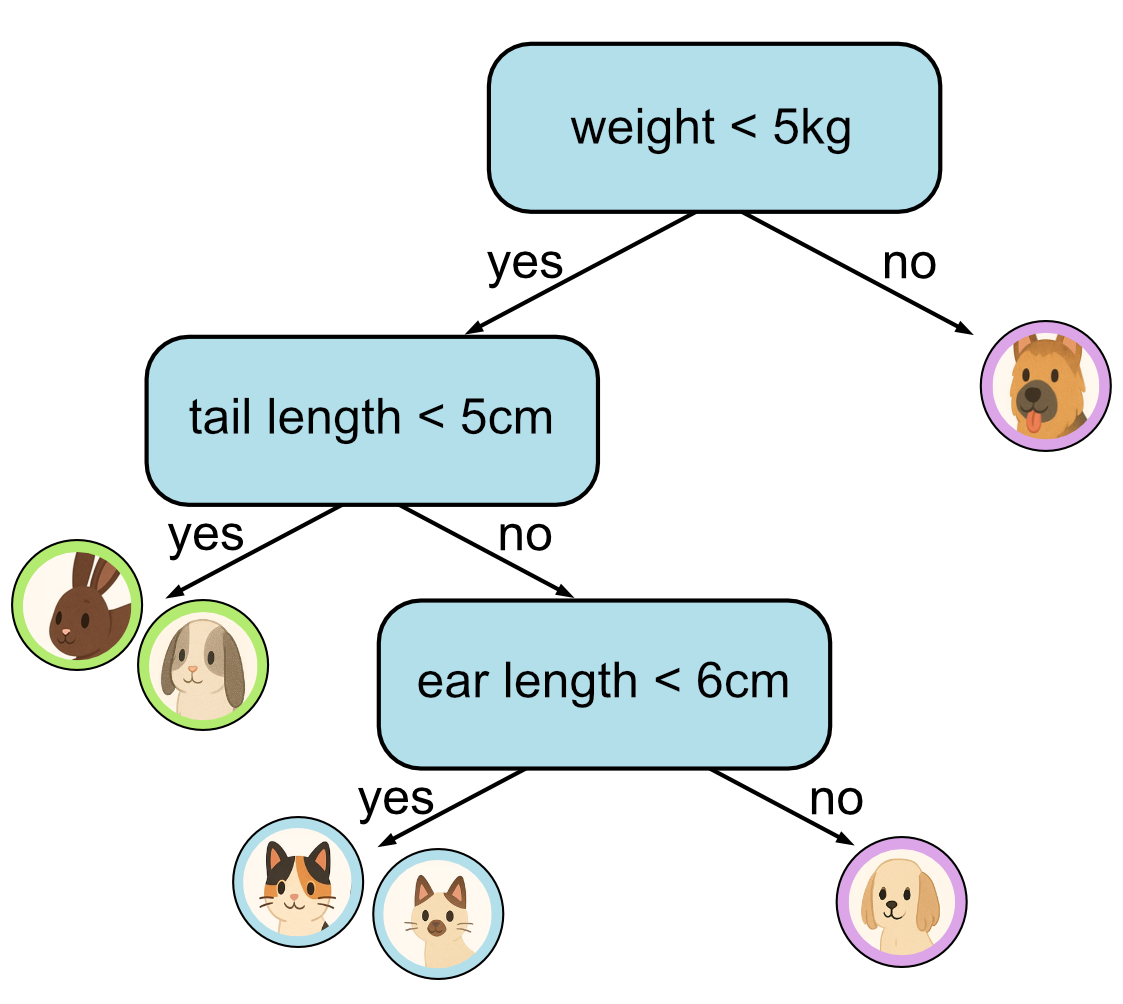
If you grow any tree large enough, you can eventually sort all the samples in the training data so that each leaf node corresponds to one class. We saw this in the previous example.
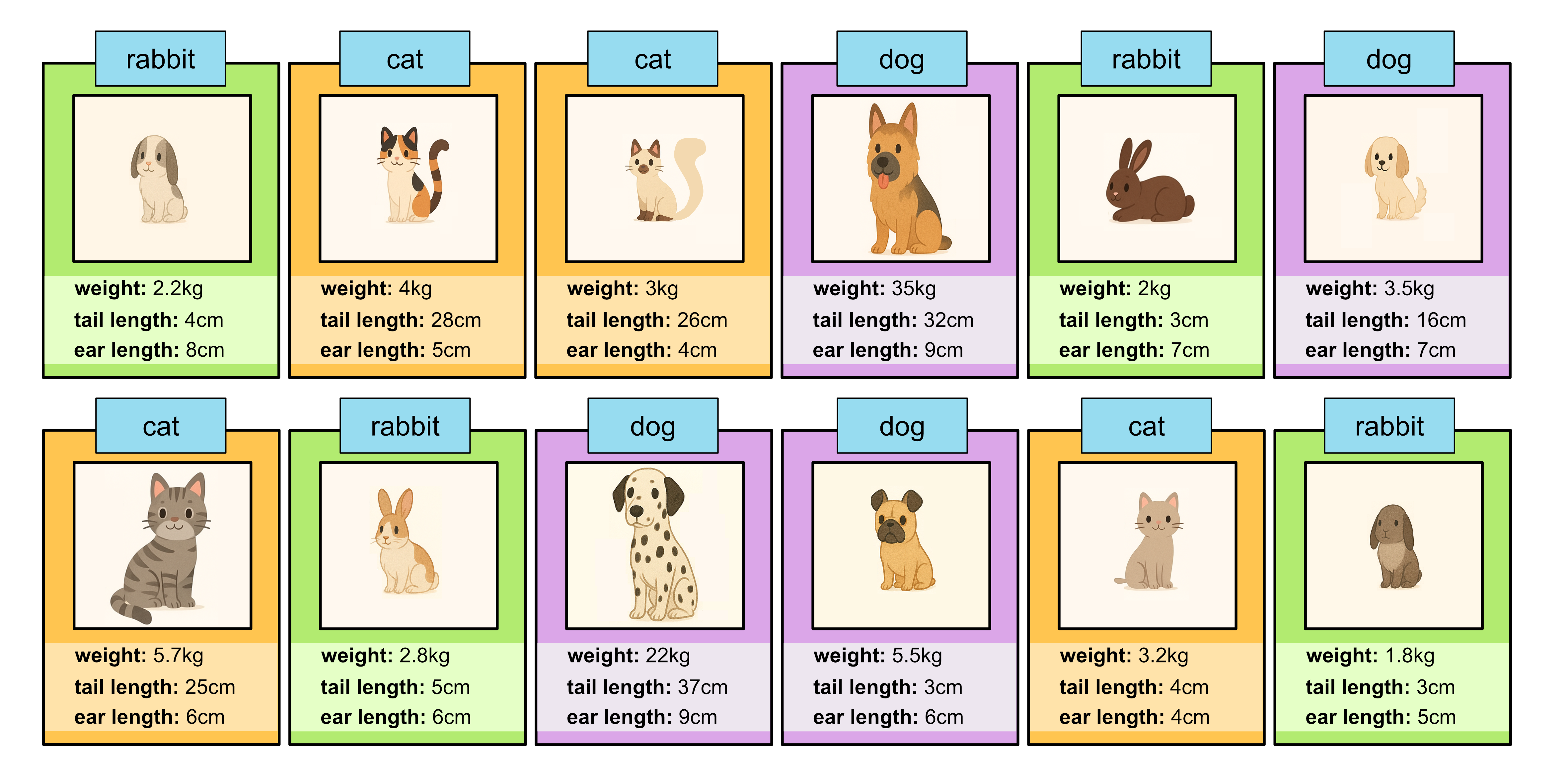
But suppose we had more training data.
Weight (kg) |
Tail Length (cm) |
Ear Length (cm) |
Class |
|---|---|---|---|
2.2 |
4 |
8 |
rabbit |
4 |
28 |
5 |
cat |
3 |
26 |
4 |
cat |
35 |
32 |
9 |
dog |
2 |
3 |
7 |
rabbit |
3.5 |
16 |
7 |
dog |
5.7 |
25 |
6 |
cat |
2.8 |
5 |
6 |
rabbit |
22 |
37 |
9 |
dog |
5.5 |
3 |
6 |
dog |
3.2 |
4 |
5 |
cat |
1.8 |
3 |
5 |
rabbit |
Since our training data is different, the tree we build will be similar, but slightly different from the one we built last time.
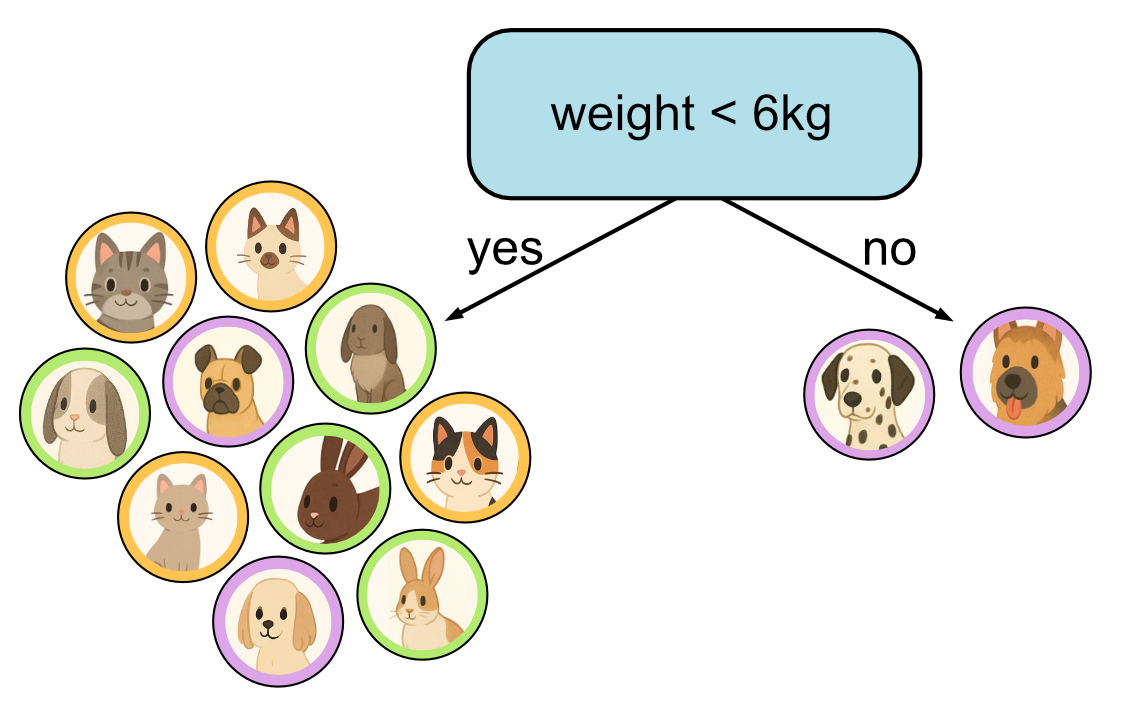
First decision.
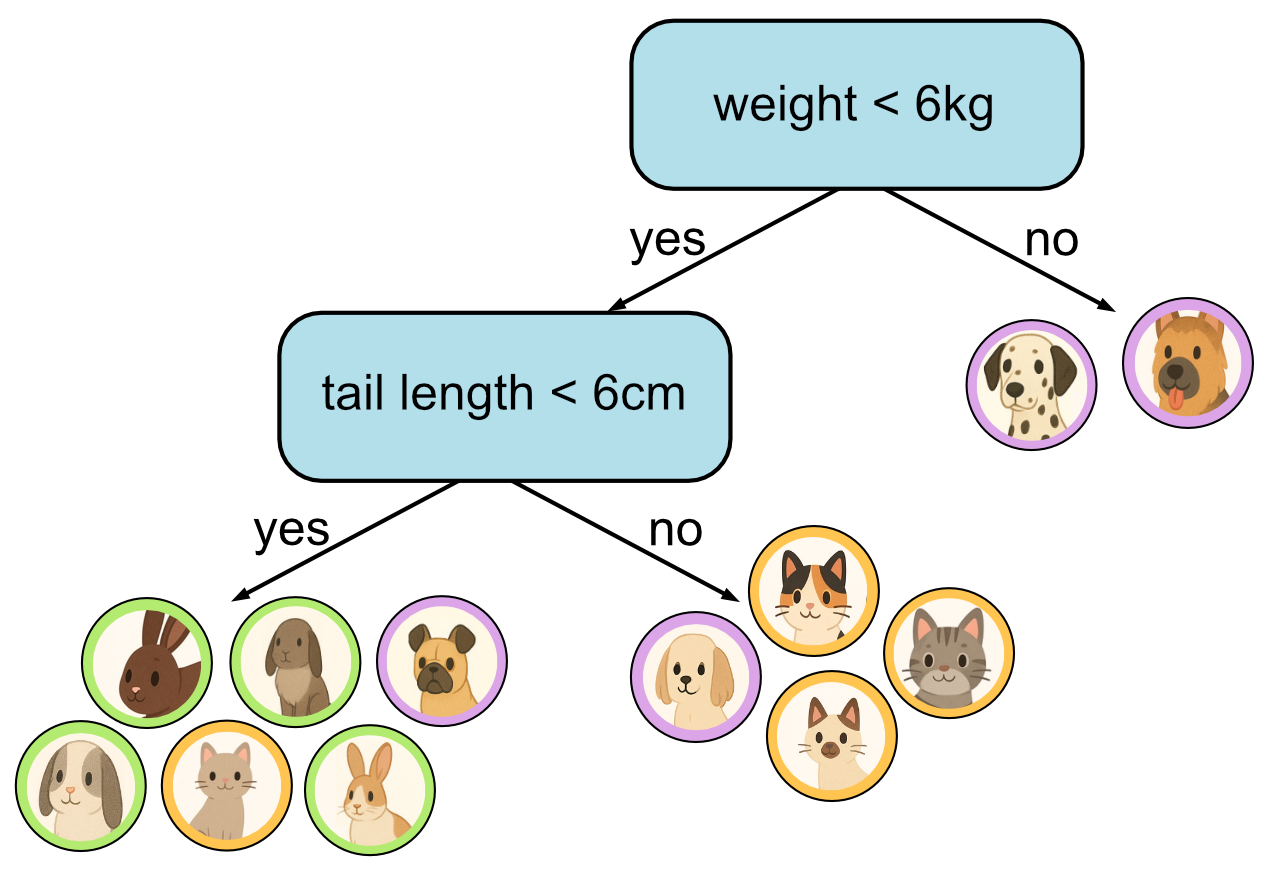
Second decision.
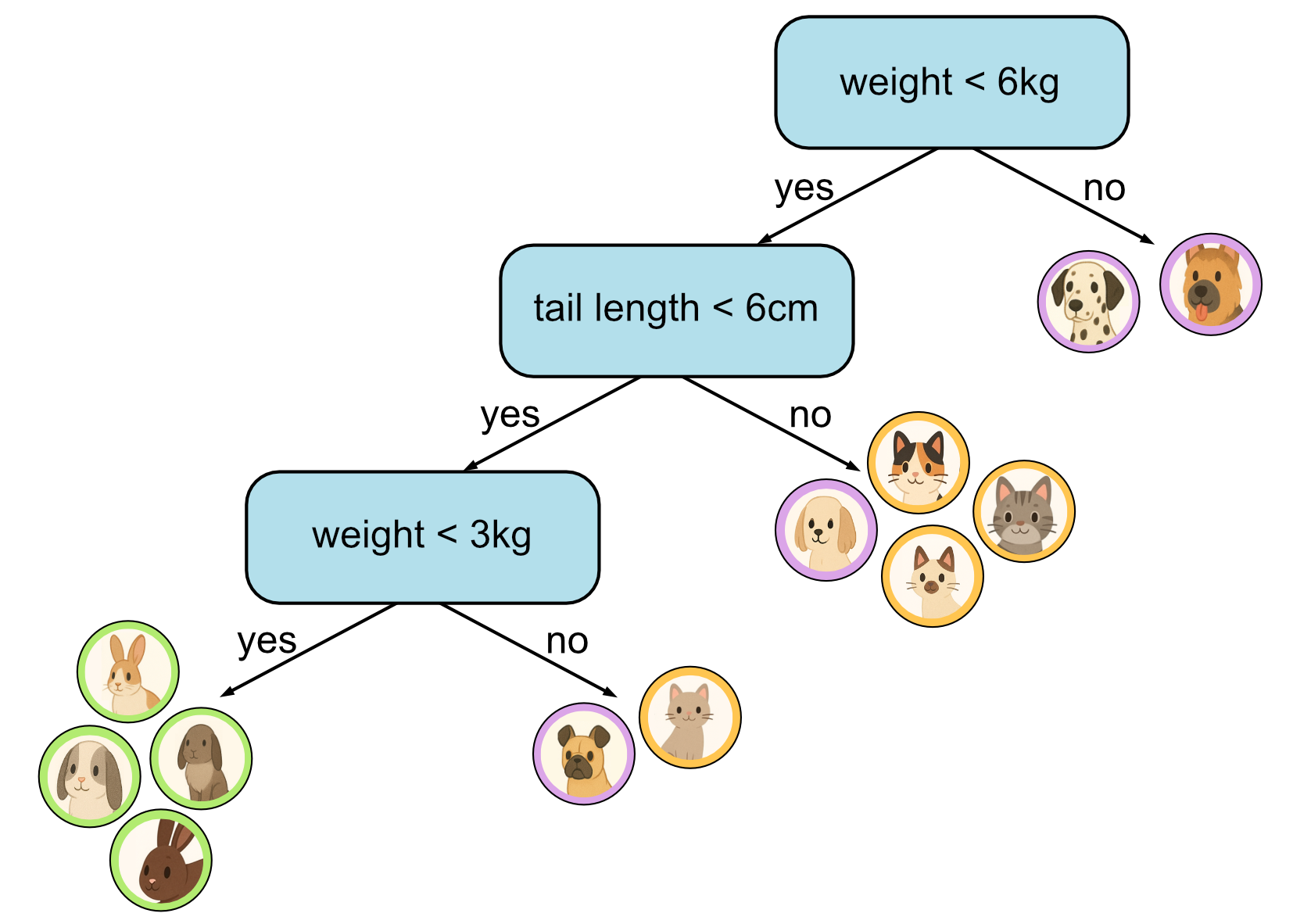
Third decision.
Fourth decision.
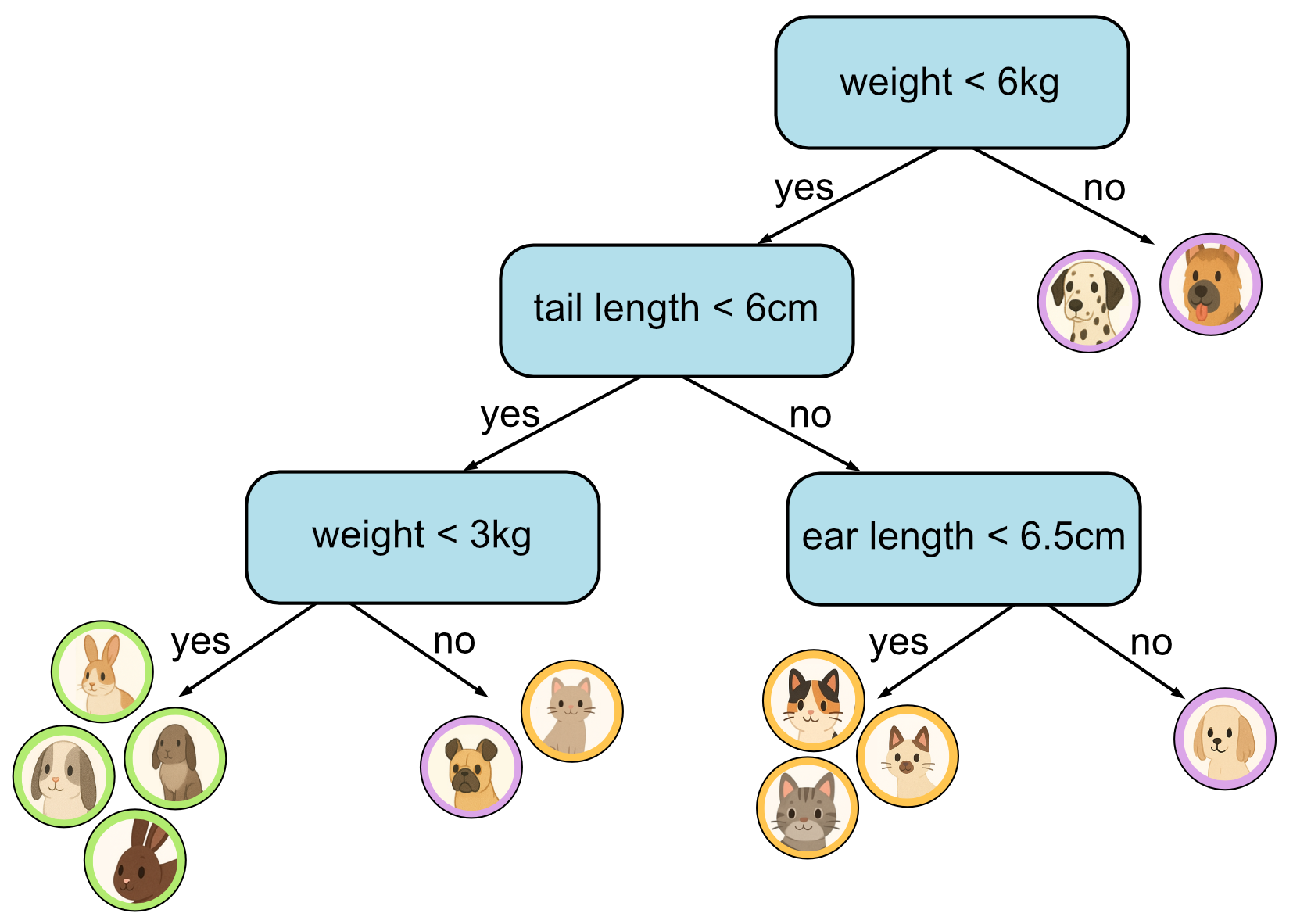
As you can see, the more training data we have, the larger our tree will tend to get. Our training data in this example only has 12 samples. In reality datasets can have hundred, thousands or even millions of samples. This means we will tend to limit the size of our tree to a fixed height. In this example we have limited the height of our tree to 3.
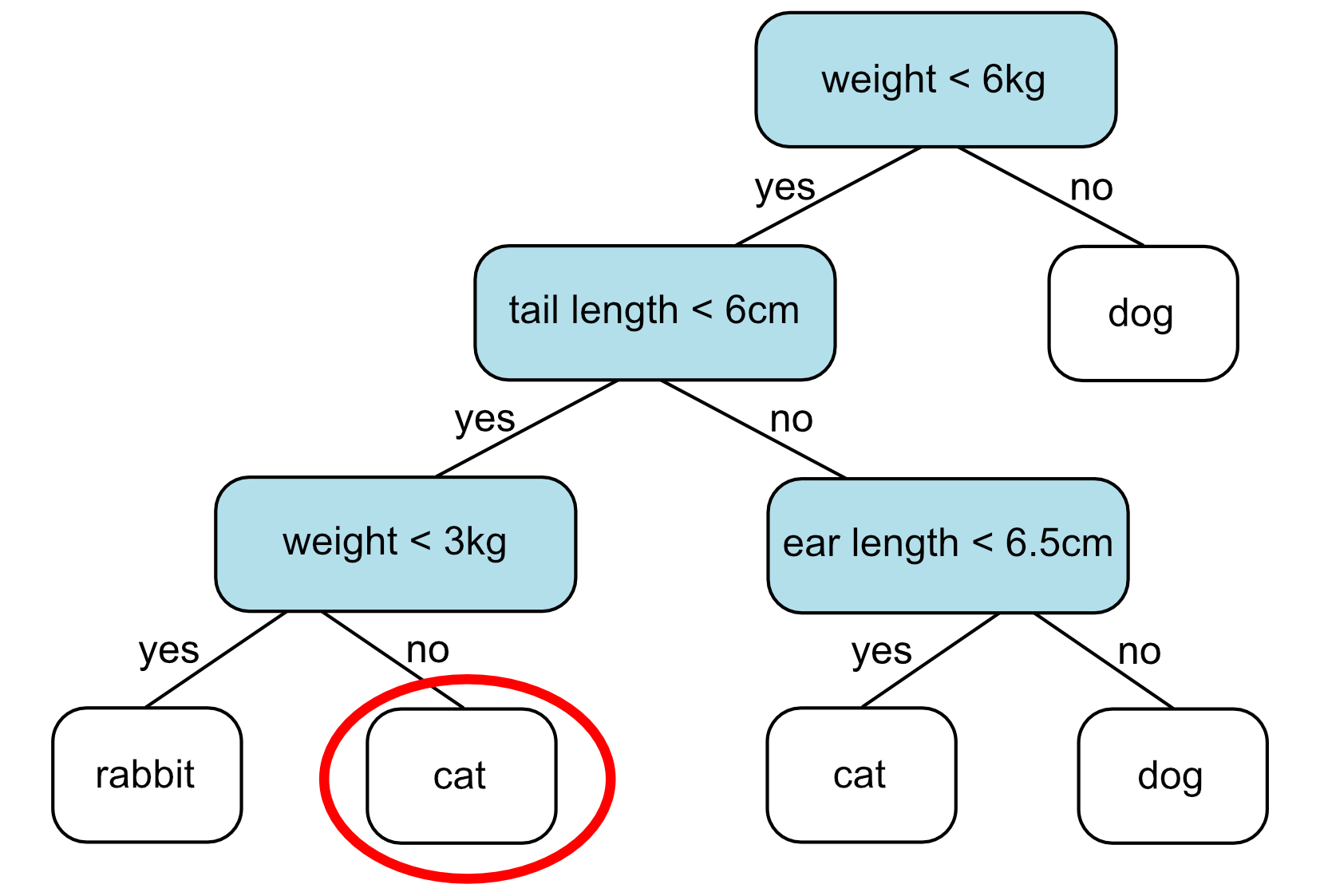
What you’ll notice is though is that this time some of our decisions don’t lead to a leaf node with a single class. This is what we call an impure node. If there are more training samples from one class that end up in this node, we label this node with the majority class. E.g. if there were two cats and one dog, we’d label this cat. In this example however, there are an equal number of dogs and cats. This is less likely to happen when there is more training data, but in this case we can choose randomly, each is equally valid. For this example, we’ll just choose cat.
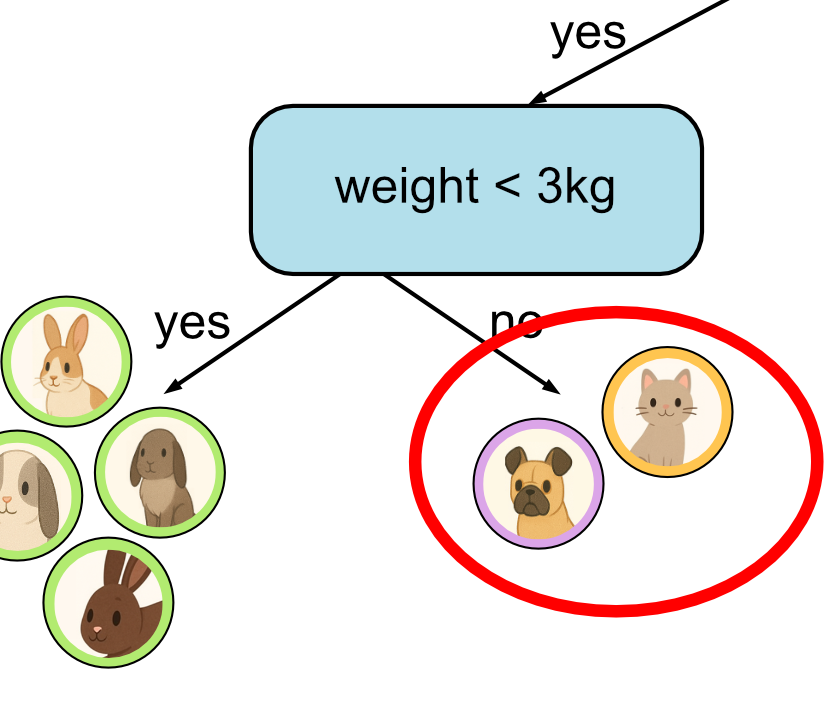
This means our final decision tree is as follows: